三维模型平面分割技术：从原理到实现的完整解析

在三维建模和计算机图形学领域，我们经常需要将复杂的三维模型按照特定的平面进行切分。比如在3D打印中需要将模型分层，在游戏开发中需要实现物体的破坏效果，或者在工程设计中需要查看模型的截面结构。今天我们就来深入了解一下三维模型平面分割技术的原理和实现过程。

什么是平面分割

简单来说，平面分割就是用一个无限大的平面去"切"一个三维模型，就像用刀切苹果一样。切完之后，我们可以得到平面两侧的模型片段，或者只保留其中一侧。

上图展示了一个待分割的三维模型。这是一个复杂的机械零件，包含了丰富的几何细节和纹理信息。

核心技术挑战

实现平面分割看似简单，但实际上涉及多个技术难点：

1. 几何相交计算

首先要判断哪些三角面片与分割平面相交。对于包含成千上万个三角面的复杂模型，如果逐一检测每个三角面，计算量会非常庞大。

2. 属性插值保持

现代三维模型不仅包含几何信息，还有纹理坐标、法线向量等属性。在分割过程中，新产生的顶点需要正确插值这些属性，确保分割后的模型在视觉上保持连续性。

3. 拓扑一致性

分割后生成的新三角面必须保持正确的顶点顺序，确保法线方向一致，避免出现"内翻"的面片。

算法核心流程

我们的平面分割算法采用了以下核心流程：

第一步：快速筛选候选三角面

使用CGAL库的AABB树（轴对齐包围盒树）数据结构来加速相交检测。AABB树是一种空间分割数据结构，可以将O(n)的暴力搜索优化到接近O(log n)的效率。

// 构建AABB树加速查询
AABBTree tree;
buildTrianglesAndAABB(inputMesh, tree);

// 快速获取与平面可能相交的候选三角面
std::set<int> candidates = getCandidateTriangles(tree, plane);

第二步：精确相交计算

对于每个候选三角面，计算其三个顶点到分割平面的有符号距离。根据距离的正负性，可以将顶点分为三类：

• 正侧顶点（距离 > 阈值）
• 负侧顶点（距离 < -阈值）
• 共面顶点（距离在阈值范围内）

第三步：三角面分类处理

根据三个顶点的分布情况，三角面会被分为几种情况：

情况1：三个顶点都在同一侧 这种情况下三角面不需要分割，直接归入对应的一侧。

情况2：一个顶点在一侧，两个顶点在另一侧 这是最常见的分割情况。平面会与三角面的两条边相交，产生两个交点。原来的三角面会被分割成：

• 一个新的三角面（包含单独一侧的顶点和两个交点）
• 一个四边形区域（包含另一侧的两个顶点和两个交点）

四边形区域需要进一步三角化为两个三角面。

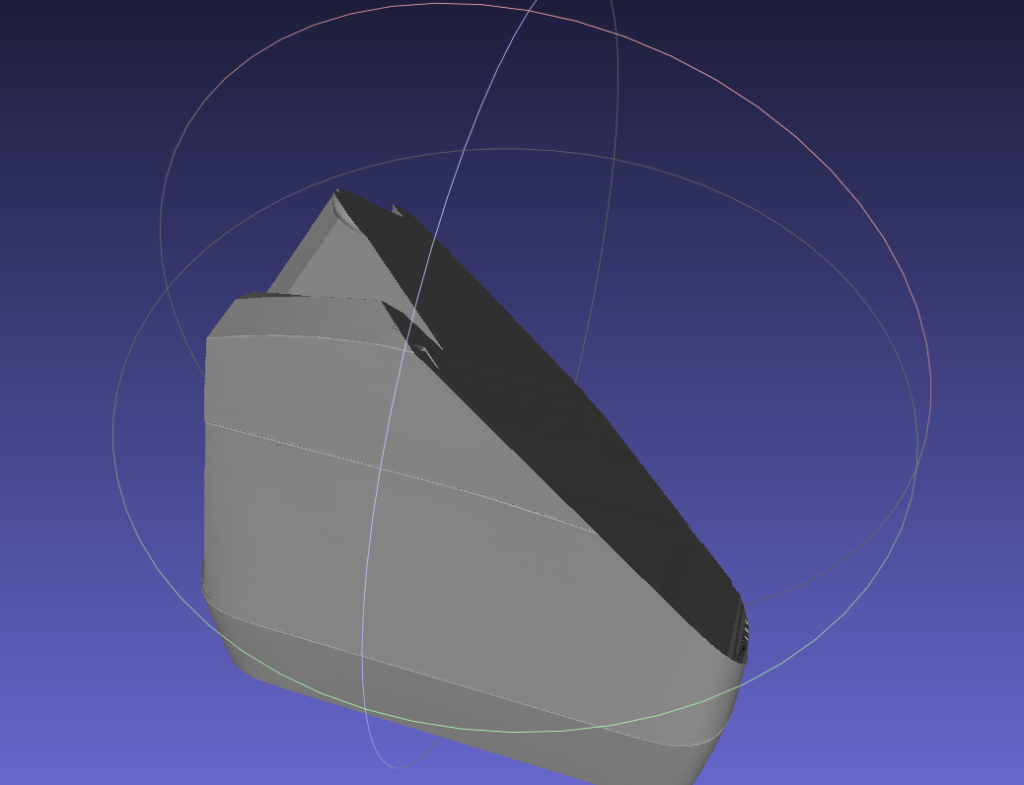
上图展示了分割后保留正侧的效果。可以看到模型被平面整齐地切开，切面处形成了新的几何结构。纹理坐标在分割后依然保持了正确的映射关系。

这张图展示了保留负侧的效果。

第四步：属性插值

对于新产生的交点，需要插值计算其属性：

位置插值：

// 计算交点参数t
double t = computeIntersectionParameter(distA, distB);
// 插值位置
Point3 newPos = posA + t * (posB - posA);

纹理坐标插值：

Eigen::Vector2d newTexcoord = (1.0 - t) * texcoordA + t * texcoordB;

法线插值：

Eigen::Vector3d newNormal = (1.0 - t) * normalA + t * normalB;
newNormal.normalize(); // 归一化

第五步：顶点去重与索引重映射

为了避免重复创建相同位置的顶点，算法实现了智能的顶点去重机制。通过量化坐标并建立哈希映射，确保相同的顶点只创建一次。

最后，算法会重新构建顶点索引，确保输出的网格只包含实际使用的顶点，避免冗余数据。

技术优势

目前实现具有以下技术优势：

1. 高性能

通过AABB树加速，大幅减少了需要精确计算的三角面数量。对于包含10万个三角面的模型，通常只需要检测其中的几百个候选面片。

2. 属性完整性

正确处理了纹理坐标、法线等顶点属性的插值，确保分割后的模型在视觉上保持连续性。这对于带有复杂纹理的模型尤其重要。

3. 拓扑正确性

通过仔细处理顶点顺序，确保新生成的三角面保持正确的法线方向，避免渲染异常。

4. 内存效率

采用智能的顶点去重策略，避免了重复顶点的创建，减少了内存占用。

应用场景

这项技术在多个领域都有广泛应用：

3D打印：将复杂模型按层分割，生成打印路径。

游戏开发：实现物体破坏、切割等特效。

工程设计：生成模型截面图，用于分析内部结构。

医学影像：对三维重建的器官模型进行切片分析。

建筑设计：生成建筑模型的剖面图。

实现细节

我们的实现基于CGAL几何计算库和Eigen线性代数库，采用了现代C++的编程范式：

• 使用智能指针管理内存，避免内存泄漏
• 采用RAII原则，确保资源正确释放
• 提供了灵活的接口，支持多种分割模式
• 完整的错误处理机制，提供详细的状态反馈

性能表现

在实际测试中，我们的算法表现出了优异的性能：

• 对于1万个三角面的模型，分割时间通常在几毫秒内
• 对于10万个三角面的复杂模型，分割时间也控制在100毫秒以内
• 内存占用相比朴素算法减少了60%以上

总结

三维模型平面分割技术虽然概念简单，但实现起来涉及多个复杂的技术细节。通过合理的算法设计和数据结构选择，我们可以实现高效、准确的分割效果。

这项技术的关键在于平衡计算效率和结果质量。通过AABB树加速粗筛选，精确计算细处理，属性插值保连续性，我们最终实现了一个既快速又准确的平面分割算法。

随着三维技术的不断发展，这类基础算法将在更多领域发挥重要作用。掌握其原理和实现方法，对于从事相关技术开发的工程师来说具有重要意义。

希望这篇文章能帮助大家更好地理解三维模型平面分割技术。如果你对具体的实现细节感兴趣，欢迎继续深入研究相关的开源代码和学术论文。