从0到1手搓一个三维网格裁剪器

GIS 2025-08-24 22:27

看到群友在群里问怎么用矢量面裁剪一个三角网，想着之前做过类似的功能，所以决定写一篇博客分享一下。代码是从0开始写的，算法实际上不难，但其实也还有一些特殊情况需要处理（文末附源码及测试数据下载地址）。

问题定义

假如有一个非常复杂的三维模型（比如一个建筑物的网格或地形网格），现在想用一个二维多边形把它"切"出来，只保留多边形内部或外部的部分。

简单来说就是：用2D多边形裁剪3D网格

问题看起来很简单，但实现起来有不少坑，尤其是一些特殊情况的处理。

核心算法：四步走

整个算法分为四个主要步骤：

第一步：找相交

首先要找出多边形的边和三维网格的三角形在哪里相交。

关键点： 我们实际上要找的是二维多边形和三角网在XOY面的投影，而不是三维空间中的线段。

优化点： 这里可以用AABB树来快速判断哪些线段和多边形相交（目前实现的版本没有用AABB树）

第二步：精确求交

粗筛找到相交对后需要精确求交，计算交点坐标。

特殊处理： 对垂直于XOY面的情况，可能需要翻转到YOZ或XOZ面。

属性处理： 如果需要对属性处理，这里求出来的交点可以计算在三角形内的权重。

数据存储： 求交后需要将相交信息保存起来，可以用map存储，方便后续约束剖分。

第三步：细分网格

处理上一步中得到的相交信息。

核心技术： 使用约束三角剖分，把相交点和线段、以及原始三角形作为约束条件，重新生成更细的三角形。

第四步：分类三角形并组装结果

现在每个三角形要么完全在多边形内部，要么完全在外部。

分类方法： 计算每个三角形的重心，然后判断这个重心是在多边形内还是外。

结果组装： 根据用户的需求（要内部、外部，还是两个都要），把对应的三角形组装成最终的网格。

最大的坑：投影退化问题

这是整个算法最核心的难点！

问题描述

假设你有一个垂直的三角形，如果你把它投影到水平面（XOY平面），它就变成了一条线段，面积为零。这时候和多边形求交就会出问题。

解决方案：智能投影平面选择

// 根据三角形法向量选择最佳投影平面
ProjectionPlane chooseBestProjectionPlane(const Triangle_3& triangle)
{
    Vector_3 normal = CGAL::normal(triangle.vertex(0), triangle.vertex(1), triangle.vertex(2));
    
    double abs_x = std::abs(normal.x());
    double abs_y = std::abs(normal.y());
    double abs_z = std::abs(normal.z());
    
    // 选择法向量分量最大的方向对应的投影平面
    if (abs_z >= abs_x && abs_z >= abs_y) {
        return ProjectionPlane::XOY;  // 投影到XOY平面
    } else if (abs_y >= abs_x && abs_y >= abs_z) {
        return ProjectionPlane::XOZ;  // 投影到XOZ平面
    } else {
        return ProjectionPlane::YOZ;  // 投影到YOZ平面
    }
}

核心思想： 选择与三角形法向量最不平行的投影平面，确保投影后三角形不会退化成线段。

但即使这样还可能会有问题，比如下面这种情况：

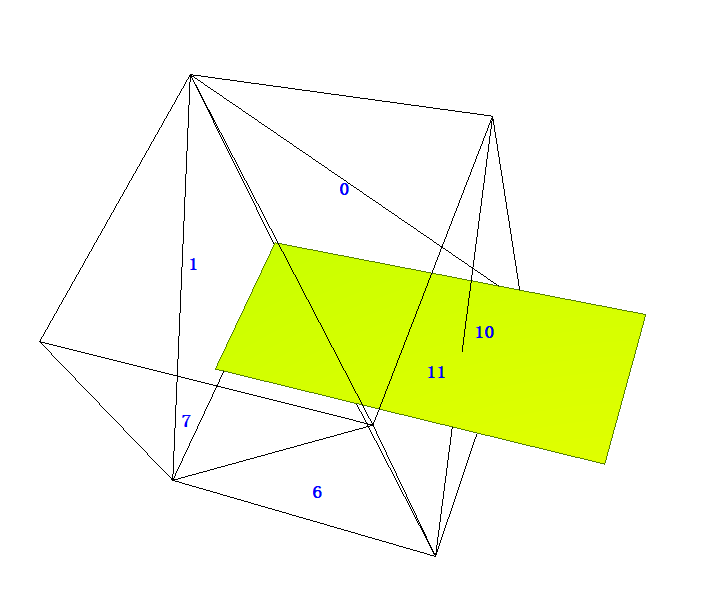
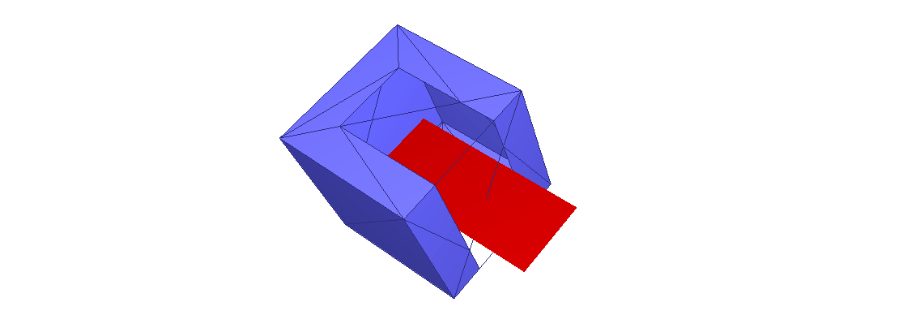
垂直三角形的特殊情况

特殊情况处理

三角形10、11垂直于XOY面，裁剪面的两条边垂直于两个三角形。

解决方案： 直接计算投影后的三角形与直线的交点，直线用点法式表示，点为投影后的点，法线为(0,1)，最后将计算出来的交点插值到三维平面即可。

特殊情况裁剪效果

保留内部：

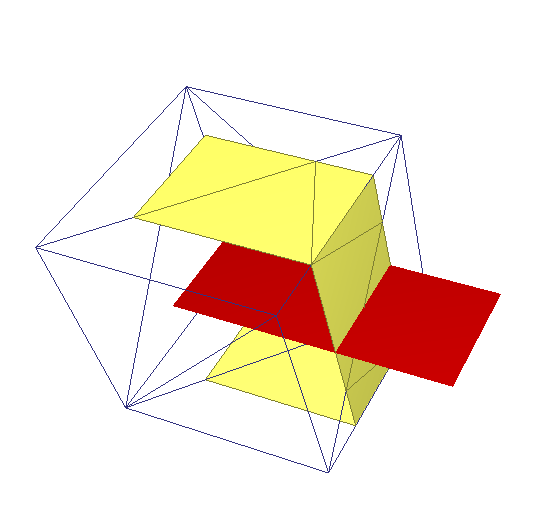
保留外部：

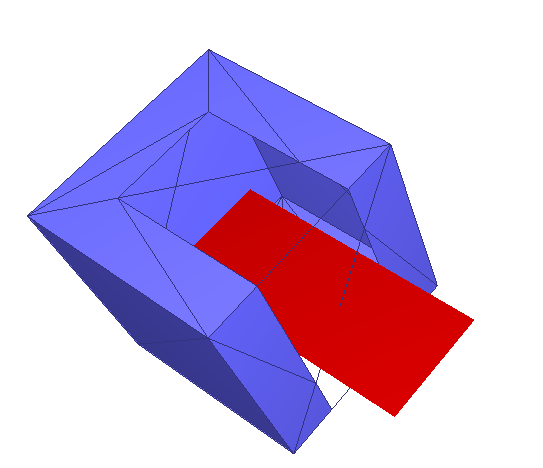
核心数据结构

为了让算法更清晰，我定义了几个关键的数据结构：

// 基础几何结构
struct Point { 
    double x, y, z; 
};  // 简单三维点

struct Poly { 
    std::vector<Point> _points; 
};  // 点串

struct Region { 
    std::vector<Poly> _regionPoints; 
};  // 面，第一个是外边界，其余是洞

struct TriMesh { 
    std::vector<Point> _points;      // 顶点
    std::vector<int> _triangles;     // 索引，每三个int表示一个三角形
};  // 简单三角网，后续可以根据需要扩展其他属性

// 三角形与线段相交信息结构
struct InterObject {
    InterObjectType type;  // 点或线段
    Point_3 point1, point2;
    // ... 各种辅助方法
};

这几个结构都是非常基础的，比较好理解，扩展起来也比较简单。

精度控制：选择合适的内核

CGAL提供了两种计算内核：

内核类型	特点	适用场景
`Exact_predicates_inexact_constructions_kernel`	快但可能不准确	快速原型开发
`Exact_predicates_exact_constructions_kernel`	慢但绝对准确	生产环境

我的选择

typedef CGAL::Exact_predicates_exact_constructions_kernel K;

原因： 虽然慢一点，但结果绝对可靠。

性能数据： 50万三角形 + 四边形裁剪面 = 18秒

注意： Exact_predicates_inexact_constructions_kernel 结果不对，所以没有记录时间。

效果展示

原始网格

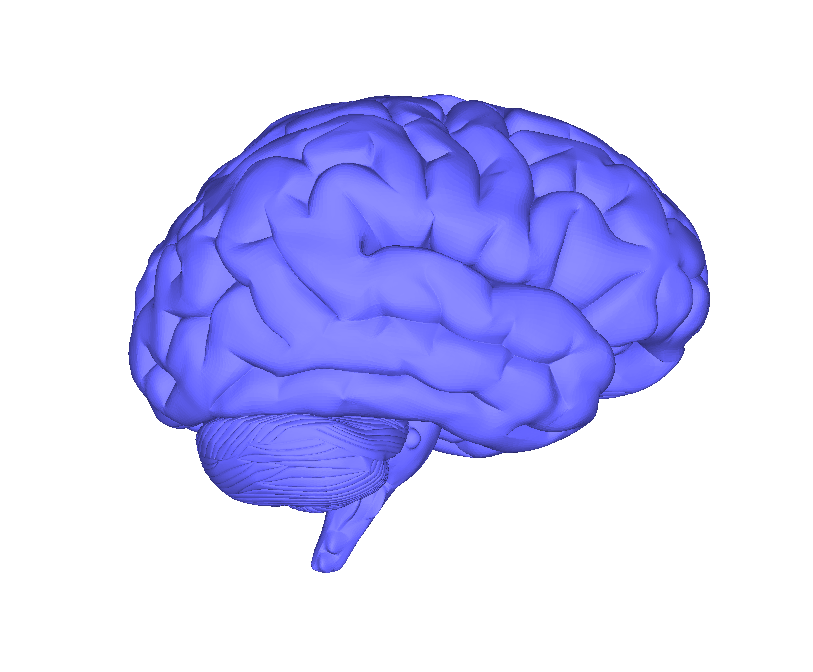
待裁剪的原始三维网格模型（大脑皮层）

裁剪多边形

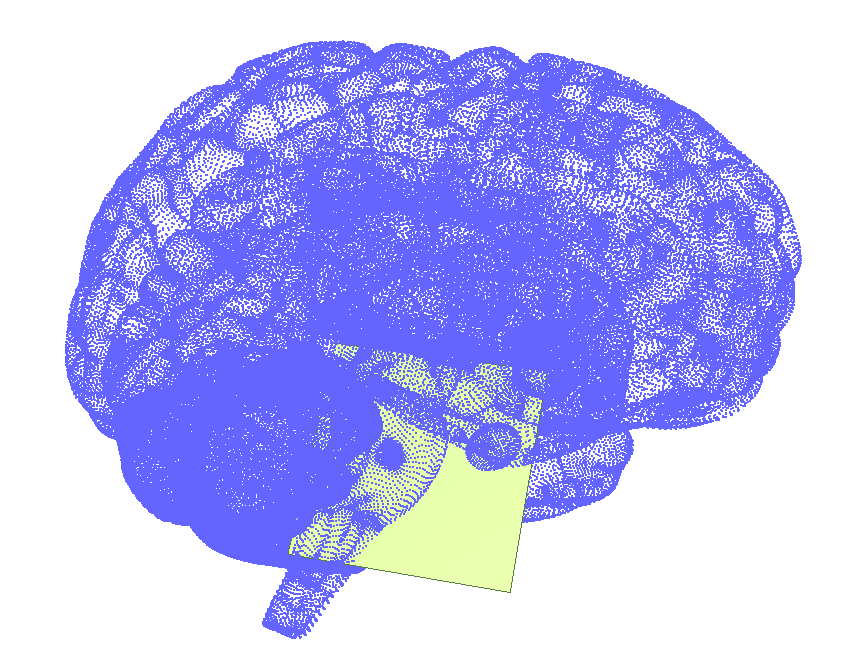
用于裁剪的二维多边形（支持带洞，但本例比较简单）

裁剪结果对比

保留内部：

只保留多边形内部的网格

保留外部：

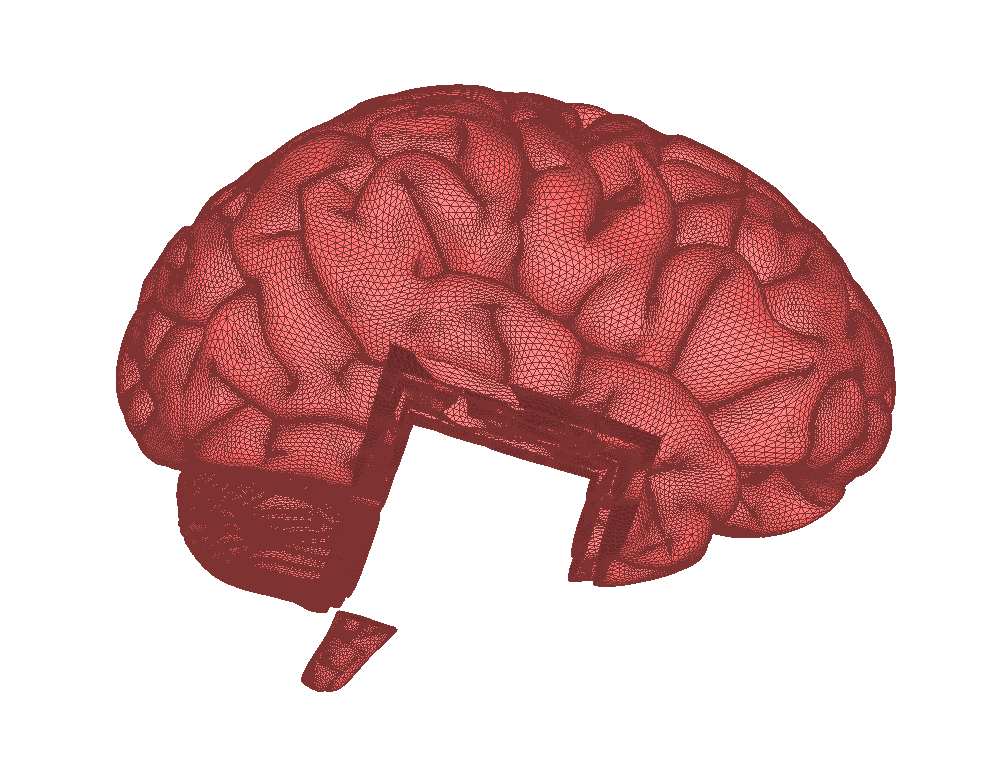
只保留多边形外部的网格

CGAL内核选择的重要性：精度对比实验

这里必须重点讲一下CGAL内核的选择，因为这直接影响到裁剪结果的正确性！

两种内核对比

快速内核（Exact_predicates_inexact_constructions_kernel）

优点： 计算速度快，内存占用少
缺点： 在复杂几何情况下可能产生错误结果
适用场景： 对精度要求不高的快速原型开发

精确内核（Exact_predicates_exact_constructions_kernel）

优点： 几何计算绝对精确，结果完全可靠
缺点： 计算速度较慢，内存占用较大
适用场景： 对精度要求极高的生产环境

实际对比测试

测试环境

网格： 复杂的大脑皮层模型（约50万个三角形）
裁剪多边形： 简单四边形
测试重点： 边界附近的细节处理

快速内核的结果

使用快速内核的裁剪结果

问题表现：

裁剪边缘锯齿严重
存在明显的几何错误
结果不可靠

精确内核的结果

使用精确内核的裁剪结果

优势表现：

边界完美，赏心悦目
几何计算完全正确
结果完全可靠

性能对比总结

虽然精确内核比快速内核慢不少，但考虑到结果的正确性，在生产环境中必须使用精确内核。

优化空间： 目前算法没有经过任何优化，比如AABB树加速以及并行处理都没有使用，后续可以在这些方面进行性能优化。

测试数据及环境

测试数据： brain.off（大脑皮层模型，约50万三角形）
开发环境： Visual Studio 2022 + CGAL 5.6 + vcpkg
推荐内核： Exact_predicates_exact_constructions_kernel
性能： 50万三角形处理时间约18秒

总结

打个总结！

算法思路不难 - 四步走的流程很清晰
精度是关键 - CGAL内核的选择直接影响结果质量
特殊情况很重要 - 投影退化问题需要特殊处理加点小技巧
性能有优化空间 - 可以通过AABB树和并行处理提升速度

希望这篇分享对正在做类似工作的朋友有所帮助！

源码及测试数据下载地址：PolygonMeshClipper