浮点数运算精度:让程序员头大的计算陷阱
一、从日常计算误区说起:为什么 0.1+0.2≠0.3?

图片来自网络,侵删
在我们的认知里,0.1+0.2 等于 0.3 是毋庸置疑的数学真理。但当我们把这个简单的计算交给计算机时,却得到了意想不到的结果。在 JavaScript 中,输入 0.1+0.2,得到的不是 0.3,而是 0.30000000000000004 。同样,在 Python、Java、C++ 等主流编程语言里,也会出现这种情况。
这并非是编程语言的缺陷,而是计算机存储和处理小数的方式导致的。计算机采用二进制存储数据,我们熟悉的十进制小数,在转换为二进制时,可能会遇到难题。就像十进制无法精确表示 1/3,只能得到 0.333... 这样的无限循环小数一样,十进制的 0.1 和 0.2 转换为二进制时,也会变成无限循环的二进制小数。
以 0.1 为例,将其转换为二进制,采用 “乘 2 取整,顺序排列” 的方法:
0.1 * 2 = 0.2,取整数部分 0,小数部分为 0.2;
0.2 * 2 = 0.4,取整数部分 0,小数部分为 0.4;
0.4 * 2 = 0.8,取整数部分 0,小数部分为 0.8;
0.8 * 2 = 1.6,取整数部分 1,小数部分为 0.6;
0.6 * 2 = 1.2,取整数部分 1,小数部分为 0.2;
可以发现,从这里开始计算陷入了循环,0.1 的二进制表示是 0.0001100110011... ,0011 会无限循环下去。同理,0.2 的二进制表示也是无限循环的。
计算机的内存是有限的,无法存储无限位的小数,只能截取并存储一个近似值。当这两个近似值相加时,最终结果自然也只是一个与 0.3 的精确二进制表示存在微小差异的近似值,这就导致了 0.1+0.2 不等于 0.3。这个看似微小的误差,在简单计算中可能被忽略,但在涉及大量运算或高精度要求的场景下,可能会累积放大,对程序的准确性产生重大影响。
二、浮点数精度的本质:IEEE 754 标准下的二进制奥秘
(一)浮点数的三要素:符号、指数与尾数
计算机中的浮点数遵循 IEEE 754 标准,这种设计使得计算机能够高效地处理各种范围的数值。浮点数由三个关键部分构成:符号位、指数位和尾数位。
符号位很简单,只用 1 位来表示这个数的正负,0 代表正数,1 则代表负数 。就像在数轴上,符号位决定了这个数是在原点的左边还是右边。
指数位的作用类似科学记数法里 10 的幂次,用来表示数值的量级。以 32 位单精度浮点数来说,它有 8 位指数位。这 8 位指数位能表示的指数范围,决定了这个浮点数可以表示非常大或者非常小的数。比如,当指数位表示的指数很大时,这个浮点数就能表示一个极大的数值;反之,当指数位表示的指数很小时,它就能表示一个极小的数值。
尾数位存储的是有效数字,就如同科学记数法里的尾数部分,反映了数值的精确程度。在 32 位单精度浮点数中,尾数位有 23 位。这 23 位的尾数,再加上一个隐含的整数部分的 1(在 IEEE 754 标准下,规范化的浮点数二进制表示形式为 1.xxx×2^n,其中 1 是隐含的,只存储小数部分 xxx),共同决定了这个浮点数的有效精度。比如,对于一个浮点数 1.2345678,在计算机中存储时,尾数位就存储了小数部分 0.2345678 的二进制表示(当然,实际存储可能会因为精度限制有截断或舍入)。
综合这三个部分,32 位单精度浮点数的表示范围大约是 ±3.4×10³⁸ ,但它的有效十进制精度仅仅约为 7 位。这意味着,在这个范围内,它最多能精确表示 7 位有效数字。这种设计是在数值范围和精度之间做了一个权衡,在满足大部分场景对数值范围需求的同时,尽量保证一定的精度。然而,也正是这种权衡,为精度误差埋下了隐患。
(二)二进制表示的天然缺陷
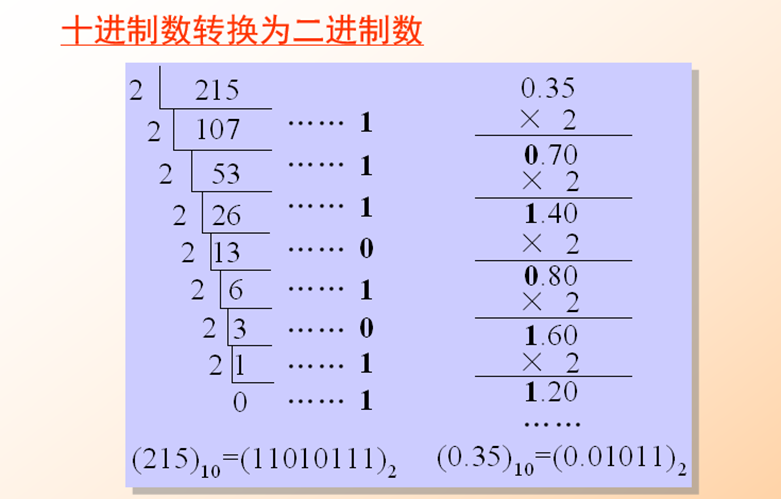
在十进制中,我们可以轻松地表示像 1/10 这样的分数,即 0.1。但当我们尝试将这个看似简单的 0.1 转换为二进制时,却会遇到麻烦。采用 “乘 2 取整,顺序排列” 的方法,将 0.1 转换为二进制的过程如下:
0.1 * 2 = 0.2,取整数部分 0,小数部分为 0.2;
0.2 * 2 = 0.4,取整数部分 0,小数部分为 0.4;
0.4 * 2 = 0.8,取整数部分 0,小数部分为 0.8;
0.8 * 2 = 1.6,取整数部分 1,小数部分为 0.6;
0.6 * 2 = 1.2,取整数部分 1,小数部分为 0.2;
可以发现,从这里开始,计算进入了一个无限循环。这表明,0.1 在二进制中是一个无限循环小数,即 0.0001100110011... 。
计算机的内存是有限的,无法存储这样无限位的小数。所以,在实际存储时,计算机只能截取有限的位数来近似表示这个小数。这样一来,存储的 0.1 的二进制值就与真实的 0.1 存在一定的偏差。同样的情况也发生在 0.2 的二进制转换中,0.2 转换为二进制也是一个无限循环小数,存储时同样会产生偏差。
当我们在计算机中进行 0.1 + 0.2 的运算时,实际上是两个存在偏差的近似值在相加。这就导致了最终的计算结果与理论上的 0.3 存在差异,我们得到的是 0.30000000000000004 这样的结果。
这种偏差在简单的计算中可能看起来微不足道,但在一些对精度要求极高的场景下,比如金融计算、科学模拟等,每次运算产生的微小偏差可能会随着计算次数的增加而不断累积放大。在金融计算中,涉及到大量资金的计算,如果每次计算都存在微小的精度误差,经过多次计算后,最终的结果可能会与实际应得的金额相差甚远,这可能会给金融机构和客户带来严重的损失。在科学模拟中,比如模拟天体的运动轨迹,如果计算过程中因为浮点数精度问题产生误差,随着时间的推移,模拟结果可能会与实际的天体运动轨迹偏差越来越大,从而影响对天体运动规律的研究和预测。
三、精度误差的连锁反应:从科学计算到 AI 训练的多米诺效应
(一)科学计算:误差累积引发的 “蝴蝶效应”
在科学计算领域,尤其是物理模拟和气象预测中,浮点数运算的精度问题犹如一颗隐藏的定时炸弹,可能引发意想不到的 “蝴蝶效应”。以求解微分方程为例,这是科学计算中常见的任务,它描述了各种物理量随时间或空间的变化规律。在实际求解过程中,由于计算机采用有限精度的浮点数来表示数值,每一步计算都会引入舍入误差。
当我们使用迭代法逐步求解微分方程时,这些微小的舍入误差会像滚雪球一样,随着迭代次数的增加而不断累积和放大。在模拟天体运动的过程中,需要精确计算天体之间的引力相互作用。如果在计算过程中使用低精度的浮点数,每一次计算引力时产生的舍入误差,经过长时间的累积,会导致模拟出的天体轨道与实际轨道产生明显的偏离。这种偏离在短时间内可能并不明显,但随着时间的推移,误差会越来越大,最终使得模拟结果完全失去参考价值。
在气象预测中,长期气候模型的预测对人类应对气候变化、制定相关政策具有重要意义。然而,研究表明,在低精度浮点运算下,长期气候模型的预测误差可能随时间呈指数增长。这是因为气候系统是一个极其复杂的非线性系统,包含了大气、海洋、陆地等多个相互作用的子系统,任何微小的误差都可能在这个复杂的系统中被放大。如果在计算大气环流、海洋温度等关键参数时存在精度误差,这些误差会通过各种物理过程相互传递和影响,最终导致对未来气候趋势的预测出现严重偏差。这不仅会影响我们对气候变化的科学认识,还可能导致基于这些预测制定的政策无法达到预期效果,甚至产生负面影响。
(二)AI 训练:精度与效率的微妙平衡
随着人工智能技术的飞速发展,AI 模型的训练成为了关键环节。而在这个过程中,浮点数精度扮演着举足轻重的角色,它直接影响着 AI 模型的训练效果和效率,其中腾讯混元团队的研究发现为这一领域提供了深刻的见解。
在神经网络训练中,浮点数的尾数位和指数位的分配就像是烹饪中的调料配比,看似细微的调整,却能对最终的 “味道”—— 模型性能产生巨大的影响。实验显示,当对输入激活值进行低精度量化时,模型损失可能增加 2% 以上。这是因为输入激活值在神经网络的信息传递中起着关键作用,低精度的量化会导致信息的丢失,使得模型在学习数据特征时出现偏差,从而影响模型的准确性和泛化能力。
然而,精度并非越高越好,在实际的 AI 训练中,还需要考虑计算效率和资源消耗。腾讯混元团队通过大量实验发现,合理分配指数位与尾数位可以在保证一定精度的同时,显著提升计算效率。例如,在 8 位总位数时采用 4 位指数 + 3 位尾数的配置,能够在不明显降低模型性能的前提下,加快计算速度,减少计算资源的占用。这一发现为 AI 硬件设计和训练优化提供了关键参考,硬件制造商可以根据这一结论设计更高效的 AI 训练芯片,而模型开发者也可以据此选择更合适的训练参数,提高训练效率,降低成本。
(三)金融计算:失之毫厘,谬以千里
金融领域对计算精度的要求堪称苛刻,任何微小的误差都可能引发严重的后果,正所谓 “失之毫厘,谬以千里”。在货币计算中,浮点数精度问题可能导致交易错误或财务报表失真,给金融机构和客户带来巨大的损失。
以利息计算和汇率转换为例,这些看似简单的操作,实际上对精度要求极高。在计算利息时,涉及到本金、利率和时间等多个参数,而且往往需要进行多次迭代计算。如果使用单精度浮点数进行计算,由于其只有 7 位精度的限制,在涉及大额资金或复杂复利计算时,很容易出现明显的偏差。假设一笔大额贷款,年利率为 5%,贷款期限为 20 年,由于单精度浮点数的精度问题,可能导致最终计算出的利息与实际应得利息相差数万元甚至更多。
在汇率转换中,全球外汇市场每天的交易量巨大,汇率的微小波动都可能导致巨额的资金变动。如果在汇率转换计算中存在精度误差,可能会使交易结果与预期相差甚远,引发交易风险。某银行系统曾因浮点数精度问题,导致客户账户余额出现分位级误差。虽然单个账户的误差看似微不足道,但当涉及大量客户时,这种误差可能会引发客户对银行的信任危机,损害银行的声誉和形象,进而影响银行的业务发展。因此,在金融计算中,必须采用高精度的计算方法和数据类型,以确保计算结果的准确性和可靠性。
四、应对精度挑战:从技术方案到实践策略
(一)数据类型选择:合适的才是最好的
在编程的世界里,选择合适的数据类型就像是为一场旅行挑选合适的装备,只有选对了,才能顺利抵达目的地。对于浮点数运算来说,不同的数据类型在精度和存储空间上各有优劣,我们需要根据具体的应用场景来做出明智的选择。
单精度(float)数据类型就像是一个小巧轻便的背包,它只占用 4 个字节的存储空间 ,适用于那些对精度要求不高、存储空间有限的场景。在游戏开发中,3D 坐标的计算就经常使用单精度浮点数。由于游戏中需要处理大量的坐标数据,对显存的占用非常敏感,使用单精度浮点数可以在允许一定误差的情况下,节省大量的显存空间,从而提高游戏的运行效率。在一些实时渲染的场景中,单精度浮点数的精度足以满足视觉上的需求,即使存在微小的误差,玩家也很难察觉。
双精度(double)数据类型则像是一个容量更大、更专业的旅行箱,它占用 8 个字节的存储空间 ,提供了大约 15 位的十进制精度。这使得它成为科学计算、金融建模等高精度场景的首选。在科学计算中,很多物理量的计算需要极高的精度,例如天体物理学中计算行星的轨道、量子力学中计算微观粒子的状态等。在金融建模中,涉及到资金的计算,任何微小的误差都可能导致巨大的损失,因此双精度浮点数的高精度特性能够确保计算结果的准确性和可靠性。在计算股票投资组合的收益时,需要精确计算每一笔交易的成本、收益以及各种手续费等,双精度浮点数可以满足这种高精度的计算需求。
对于那些需要超越双精度的场景,比如密码学、天文计算等,就需要借助高精度库的力量了。GMP(GNU Multiple Precision Arithmetic Library)和 MPFR(Multiple Precision Floating-Point Reliable Library)等库就像是专业的探险装备,它们支持任意精度的浮点运算。在密码学中,为了保证加密算法的安全性,需要进行大量的大数运算,这些运算对精度的要求极高,普通的浮点数类型无法满足。GMP 库提供了高效的大数运算函数,可以处理任意大小的整数和浮点数,确保加密和解密过程的准确性和安全性。在天文计算中,计算星系的演化、黑洞的形成等复杂的天体物理过程,也需要高精度的计算,MPFR 库能够提供所需的精度支持,帮助科学家们更准确地模拟和研究这些天体现象。
(二)算法优化:规避误差的 “避坑指南”
在进行浮点数运算时,我们就像是在布满陷阱的道路上行走,一个不小心就可能陷入误差的泥沼。因此,掌握一些算法优化的技巧,就像是拥有了一份 “避坑指南”,能够帮助我们避开那些常见的误差陷阱。
直接比较浮点数相等就是一个常见的陷阱。由于浮点数在存储和运算过程中存在舍入误差,两个看似相等的浮点数,实际上可能存在微小的差异。因此,在判断两个浮点数是否相等时,不能直接使用 “==” 运算符,而应该使用容差范围来判断。具体来说,就是计算两个浮点数的差值的绝对值,如果这个绝对值小于一个预先设定的容差(如 1e-8),就认为这两个浮点数在一定精度范围内是相等的。在进行数值模拟时,经常需要判断两个物理量是否相等,如果直接使用 “==” 运算符,可能会因为浮点数的精度问题导致判断错误,而使用容差范围进行比较则可以避免这种情况。
减少大数运算与累积误差也是非常重要的。在进行一系列浮点数运算时,先进行小数运算,避免先加总大数后加小数导致的 “大数吃小数” 现象。当一个很大的数和一个很小的数相加时,如果先将大数加总,再加上小数,由于浮点数的精度有限,小数部分可能会被忽略,从而导致计算结果出现较大的误差。为了减少这种误差,可以采用 Kahan 求和算法,该算法通过动态补偿舍入误差,能够有效地提高求和运算的精度。在计算一系列物理量的总和时,使用 Kahan 求和算法可以减少累积误差,使计算结果更加准确。
在进行浮点数运算时,还需要合理处理边界情况,注意非规范数(Subnormal Numbers)、无穷大、NaN(非数值)等特殊值。非规范数是指那些绝对值非常小的数,它们的指数部分为全 0,尾数部分不为 0,在运算中可能会导致精度损失。无穷大表示超出了浮点数能够表示的范围,而 NaN 则表示一个未定义或非法的数值。在进行除法运算时,如果除数为 0,结果可能会是无穷大或 NaN;在进行一些复杂的数学运算时,也可能会产生非规范数。因此,在编写代码时,需要对这些特殊值进行特殊处理,避免运算中出现未定义行为。在进行金融计算时,如果出现无穷大或 NaN,可能会导致交易系统出现错误,因此需要在代码中进行严格的检查和处理。
(三)工程实践:全流程精度管控
在实际的工程项目中,对浮点数精度的管控需要贯穿整个项目的生命周期,从需求分析到编码实现,再到测试验证,每一个环节都至关重要。
在需求分析阶段,明确业务对精度的要求是首要任务。不同的业务场景对精度的要求千差万别,在金融计算中,通常需要精确到分位,因为涉及到资金的交易,任何微小的误差都可能导致财务损失;在物理模拟中,可能需要保留 6 位有效数字,以保证模拟结果的准确性和可靠性。只有明确了这些精度要求,我们才能在后续的设计和实现中选择合适的数据类型和算法,确保系统能够满足业务需求。在设计一个财务系统时,需要与业务团队沟通,了解每一项业务操作对精度的具体要求,然后根据这些要求来选择合适的数据类型和计算方法。
编码阶段是将需求转化为实际代码的关键环节。在这个阶段,我们应该优先使用双精度类型,以提供更高的精度保障。对于一些关键的计算,一定要添加注释说明精度处理逻辑,这不仅有助于自己和团队成员理解代码的含义,也方便后续的维护和调试。“使用容差比较,允许 1e-6 误差” 这样的注释,可以让其他开发人员清楚地知道这段代码在处理浮点数相等判断时的精度策略。在编写一个复杂的数学计算函数时,详细的注释可以帮助他人快速理解函数的功能和精度处理方式,提高代码的可读性和可维护性。
测试阶段是验证系统精度是否符合要求的最后一道防线。在这个阶段,我们需要设计边界值测试用例,验证极端场景下的精度表现。极大数与极小数的运算、多次迭代后的误差累积等情况都需要进行严格的测试。通过这些测试,可以发现代码中潜在的精度问题,并及时进行修复。在测试一个科学计算程序时,可以设计一系列边界值测试用例,包括输入极大数和极小数,观察计算结果是否正确;进行多次迭代计算,检查误差是否在可接受的范围内。只有通过充分的测试,才能确保系统在各种情况下都能稳定、准确地运行。
五、最后:让计算误差 “可控” 而非 “可怕”
浮点数精度问题并非无法逾越的障碍,而是计算机数值计算的固有特性。通过理解 IEEE 754 标准的底层逻辑,针对不同场景选择合适的数据类型和算法,我们完全能够将误差控制在可接受范围内。无论是科学研究中的精确模拟,还是商业系统中的可靠计算,关键在于建立 “精度意识”—— 在追求计算效率的同时,不忽视每一个可能影响结果的微小误差。毕竟,真正可靠的程序,往往赢在细节的把控上。